| Mensuration 2D | RI AMIN SFC ARI ICDS SUPERVISOR |

by

1. The diagonal of square is 20 cm, then perimeter of the square must be:
  • 10 √2 cm
  • 40 cm
  • 200 cm
  • 40 √2 cm

Correct Answers Is: 4
SOLUTION
Given:

The diagonal of the square is 20 cm.

Concept used: 

Perimter = 2√2 x diagonal

Calculation: 

⇒ Perimeter = 2√2 x 20 = 40√2 cm

∴ The diagonal of square is 20 cm, then perimeter of the square must be 40 √2 cm.

2. A field measures 90 m by 60 m. There is a concrete path 3 m wide all around its perimeter. Find the total area covered by the concrete path.
  • 963 m2
  • 639 m2
  • 936 m2
  • 693 m2

Correct Answers Is: 3
SOLUTION
As we know,

Area of the rectangle = length × breadth

Length of the field = 90 m

Breath of the field = 60 m

⇒ Area of the field = 90 × 60 = 5400 m2

Length of the field including path = 90 + 6 = 96 m

Breadth of the field including path = 60 + 6 = 66 m

⇒ Area of the field including path = 96 × 66 = 6336 m2

∴ Area of the path = 6336 – 5400 = 936 m2

3. A wire is in the form of a square with side 66 cm. If it is bent into a circle, then what is the radius of the circle?
  • 42
  • 36
  • 45
  • 33

Correct Answers Is: 1
SOLUTION
Given:

A wire is in the shape of a square of side 66 cm

Formula Used:

The perimeter of a Square = 4 × Side

The perimeter of a Circle = 2πr

Calculation:

According to the question,

Perimeter of Square = Perimeter of Circle

⇒ 4 × 66 = 2 × (22/7) × r

⇒ 2 × 3 = r/7

⇒ r = 42 cm

∴ The radius of the circle is 42 cm.

4. Find the area of a scalene triangle whose sides are 8 cm, 5 cm, and 9 cm. 
  • 7√6
  • 6√11 
  • 5√8
  • 8√2

Correct Answers Is: 2
SOLUTION
Given:

The sides of a scalene triangle a = 8 cm, b = 5 cm, c = 9 cm

Formula used:

Using heron’s formula = √s × (s – a) × (s – b) × (s – c)

Where, S = semi – perimeter and a, b & c are the sides of the triangle

S = (a + b + c)/2

Calculation:

Here semi – perimeter (s) = (8 + 5 + 9)/2 = 11 cm

Using heron’s formula,

 Area of the triangle = √s × (s – a) × (s – b) × (s – c)

⇒ √11 × (11 – 8) × (11 – 5) × (11 – 9)

⇒ √11 × 3 × 6 × 2

⇒ √396

⇒ 6√11 cm

∴ The correct answer is 6√11 cm.

5. If the side of square is increased by 5 cm, the area increased by 165 sq.cm. The side of the square is: 
  • 12 cm.
  • 13 cm.
  • 14 cm.
  • 15 cm.

Correct Answers Is: 3
SOLUTION
Given:

If the side of the square is increased by 5 cm, the area increased by 165 sq.cm.

Formula Used:

Area of square = Side2

Calculation:

Let each side of the square be x.

⇒ (x+5)2 – x2 = 165

⇒ x2 + 25 +10x – x2 = 165

⇒ 10x +25 = 165

⇒ 10x = 140

⇒ x = 14.

∴ The side of the square is 14 cm.

6. The base of a triangle is half the base of a parallelogram having the same area as that of the triangle. The ratio of the heights of the triangle to the parallelogram will be:
  • 1 : 4
  • 4 : 1
  • 2 : 1
  • 1 : 2

Correct Answers Is: 2
SOLUTION
Let the base of parallelogram = b

⇒ Base of triangle = b/2

Let the height of parallelogram be h1 and height of triangle be h2

Given that the area of parallelogram is equal to area of triangle

⇒ 1/2 × b/2 × h2 = b × h1

∴ h2 ∶ h1 = 4 ∶ 1

7. The sides of a triangle are in the ratio 4 : 9 : 7. If the sum of the shortest and the longest sides is 65 cm, then what is the length of the third side? (in cm)
  • 35 cm
  • 30 cm
  • 55 cm
  • 33.5 cm

Correct Answers Is: 1
SOLUTION
Given:

The sides of a triangle are in the ratio 4 : 9 : 7

The sum of the shortest and the longest sides is 65 cm.

Calculation:

Shortest side of the triangle = 4 units

Longest side of the triangle = 9 units

The sum of the shortest and the longest sides = 4 + 9

⇒ 13 units

According to the question,

13 units = 65 cm

So, 1 unit = 5 cm

Length of the third side = 7 × 5

⇒ 35 cm

∴ The required answer is 35 cm.

8. The length of the base of a triangle is 6 cm more than the corresponding altitude. If the area of the triangle is 108 cm2, find the length of the base of the triangle.
  • 12 cm
  • 9 cm
  • 18 cm
  • 27 cm

Correct Answers Is: 3
SOLUTION
Given:

The length of the base of a triangle is 6 cm more than the corresponding altitude.

Area of the triangle = 108 cm2

Concept used:

Area of a triangle = 1/2 × b × h

b = base

h = height or altitude

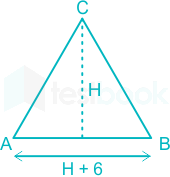
Calculation:

Let the altitude be H cm

So, base = (H + 6) cm

According to the question,

1/2 × H × (H + 6) = 108

⇒ H2 + 6H – 216 = 0

⇒ H2 + 18H – 12H – 216 = 0

⇒ H(H + 18) – 12(H + 18) = 0

⇒ (H + 18)(H – 12) = 0

H = – 18, 12

Length cannot be negative so H = 12

So, base = 12 + 6 = 18 cm

∴ The length of the base of the triangle is 18 cm

9. If the area of triangle is 250m2 and the ratio of the base and the height is 4 ∶ 5, then find its height.
  • 25 m
  • 20 m
  • 30 m
  • 24 m

Correct Answers Is: 1
SOLUTION
Given:

Area of a triangle = 250 m2

Base : Height = 4 : 5

Formula used:

Area of a triangle = (1/2) × base × height

Calculation:

Let the base be 4x

Then height = 5x

Area of a triangle = 250 m2

⇒ (1/2) × 4x × 5x = 250

⇒ 10x2 = 250

⇒ x = 5

Height = 5x = 25 m

10. A rectangular filed had length 32 cm and breadth 20 cm. How many square tiles of 4 cm should be used to cover the rectangular field?

  • 40
  • 45
  • 37
  • 42

Correct Answers Is: 1
SOLUTION
Given:

Length of rectangular field = 32 cm

Breadth of rectangular field = 20 cm

Length of tile = 4 cm

Formula Used:

Area of square = side × side

Area of rectangle = length × breadth

Calculations:

Length of rectangular field = 32 cm

Breadth of rectangular field = 20 cm

Length of tile = 4 cm

⇒ Area of rectangular field = (32 × 20) = 640 cm2

Area of each tile = (4 × 4) = 16 cm2

⇒ Number of tiles = (640/16) = 40

∴ The number of square tiles used to cover the rectangular field is 40.

11. On increasing the diameter of a circle by 40%, its area will be increased by 
  • 40%
  • 80%
  • 96%
  • 82%

Correct Answers Is: 3

12. The cost of laying the carpet is ₹ 10/m2. Find the cost of laying carpet on a triangular field having sides 10m, 20m & 20m.
  • 900
  • 250 √15
  • 150 √15
  • 350 √15

Correct Answers Is: 2

13. What is the area of an equilateral triangle whose each sides is 12 cm?
  • 36√3 cm2
  • 38√3 cm2
  • 34√3 cm2
  • 40√3 cm2

Correct Answers Is: 1
SOLUTION
Given: 

Side of equilateral triangle = 12 cm

Formula used:

Area = (1/4) × a2 × √3

Calculations:

According to the questions,

⇒ Area = (1/4) × (12)2 × √3

⇒ Area = (1/4) × 144 × √3

⇒ Area = 36 × √3 = 36√3 cm2 

∴ The area of an equilateral triangle will be 36√3 cm2.

14. The area of a rectangle is 252 cm2. If its length is 18 cm, then what is its perimeter (in cm)?
  • 62
  • 68
  • 64
  • 66

Correct Answers Is: 3
SOLUTION
Given: 

Area of a rectangle = 252 cm2

Length of the rectangle = 18 cm

Concept used:

Area of rectangle = Length x Breadth

Perimeter of rectangle = 2 x (Length + Breadth)

Calculation:

Let the breadth of the rectangle be b cm. 

According to the question,

⇒ 252 = 18  x b

⇒ b = 252/18 = 14 cm

So, the breadth of the rectangle is 14 cm.

Now,

Perimeter of the rectangle

⇒ 2 x (18 + 14)

⇒ 2 x 32 = 64 cm

∴ The perimeter of the rectangle is 64 cm.

15. What is the area of a square whose diagonal measures 4 cm?
 
  • 10 cm2
  • 8 cm2
  • 6 cm2
  • 4 cm2

Correct Answers Is: 2
SOLUTION
Given:

Diagonal = 4 cm

Formula Used:

Area = (side)2

Diagonal = √2 × side

Calculation:

4 = √2 × side

⇒ side = 2√2 cm

∴ Area of the square = (2√2)2 = 8 cm2

16. A copper wire when bent in the form of a square encloses an area of 121 cm2. If the same wire is bent in the form of a circle, find the area of the circle. (Use π = 22/7)
  • 154 cm2
  • 153 cm2
  • 155 cm2
  • 150 cm2

Correct Answers Is: 1
SOLUTION
Area of square = 121 cm2

Let the side of square be ‘a’ cm,

⇒ a2 = 121 cm2

⇒ a = 11 cm

Now, the length of the wire = Perimeter of square

⇒ Length = 4 × 11 = 44 cm

Also, Length of wire = Perimeter of circle

⇒ 2πr = 44 cm

⇒ 2 × 22/7 × r = 44 cm

⇒ r = 7 cm

Area of circle = πr2

∴ Area = 22/7 × 7 × 7 = 154 cm2

17. The ratio of the outer and inner perimeters of a circular path is 23 ∶ 22. If the path is 5 mtr wide, the diameter of the inner circle is?
  • 55 mtr
  • 110 mtr
  • 220 mtr
  • 230 mtr

Correct Answers Is: 3
SOLUTION
Given:

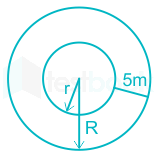
The ratio of outer and inner perimeters of a circular path = 23 ∶ 22

The path is 5 m wide.

Concept used:

Circumference of circle = 2πr

Diameter = 2 × Radius

Calculation:


18. The area of a circle is 100 times the area of another circle. The ratio of their circumferences is:
  • 10 ∶ 1
  • 5 ∶ 1
  • 22 ∶ 7
  • 50 ∶ 1

Correct Answers Is: 1
SOLUTION
Given:

The area of one circle is 100 times the area of another circle.

Formula used:

Area of Circle = πr2

Circumference of circle = 2πr

r = radius 

Calculations:

Let the radius of the circles be r1 and r2

According to the question,

π(r1)2 = 100 × π(r1)2

⇒ (r1/r2)² = (100)

⇒ r1/r2 = 10

Ratio of their circumferences = 2πr1/2πr2 = r1/r2 = 10

Hence, The Required ratio is 10.

19. A rectangular park is 40 meter long and 25 meter wide. A path 2.5 meter wide is constructed outside the park. Find the area of the path:
  • 400 m2
  • 450 m2
  • 350 m2
  • 250 m2

Correct Answers Is: 3
SOLUTION
Given:

Length of park = 40 m

Breadth = 25 m

A 2.5 m wide path is constructed outside the park

Formula Used:

Area of park = l x b

Calculations:

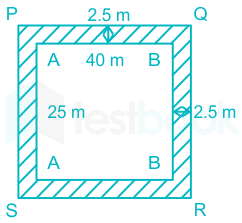
According to the formula,

Area of park = l x b = 40 x 25 = 1000 m2

Area of park with a path will be

⇒ Length changes to = 40 + 2.5 + 2.5 = 45 m

⇒ Breadth changes to = 25 + 2.5 + 2.5 = 30 m

⇒ Area of park with path = 45 x 30 = 1350 m2

So, the Area of the path will be

Area of  path = Area of the park with path – Area of park

⇒ 1350 – 1000 = 350 m2

∴ The area of the path is 350 m2

20. The areas of two circles are in the ratio 1 ∶ 2. If the two circles are bent in the form of squares, what is the ratio of their areas?
  • 1 ∶ 2
  • 1 ∶ 3
  • 1 ∶ √2
  • 1 ∶ 4

Correct Answers Is: 1
SOLUTION
Formula used:

Area of circle = πr2

Area of square = (side)2

Calculation:

Let the radius of smaller and larger circles be r and R respectively and the sides of smaller and larger squares be a and A respectively.

Area of smaller circle = πr2 = 1

⇒ r = 1/√π 

Circumference of smaller circle = Circumference of smaller square 

⇒ 2πr = 4a

⇒ a = √π/2       

Area of smaller square

⇒ a2 = π/4           ———-(1)

Area of larger circle = πR2 = 2

⇒ R = √2/√π 

Circumference of larger circle = Circumference of larger square 

⇒ 2πR = 4A

⇒ A = 

Area of larger square 

⇒ A2 = 2π/4 = π/2    ———-(2)

from equation (1) & (2)

⇒ 

∴ The correct answer is 1 : 2.

OSSSC RI,ARI,AMIN,SFS,ICDS Supervisor -2024

Download Our App for Quiz .

Quiz available at APTITUDE_ Mensuration 2D – Level 1 & 2

Download App For Quiz

Subscribe Us

Facebook Twitter Youtube Telegram Instagram

Leave a Comment